 |
Анализ спектра методом ДПФ |
При исследовании несинусоидальных сигналов может потребоваться их спектральный анализ. По ряду дискретных отсчётов, методом дискретного преобразования Фурье, можно рассчитать гармонический спектр исследуемой функции. Подробнее ознакомиться с методами спектрального анализа можно ознакомиться в 5 главе книги Дьяконова В. П. "Расчет нелинейных и импульсных устройств на программируемых микрокалькуляторах" М.: Радио и связь, 1984.
Спектр периодических сигналов определяется в усечённый m членами ряд Фурье исследуемой функции, которая задаётся N дискретными отсчётами, 1...N. Этот ряд имеет следующий вид:
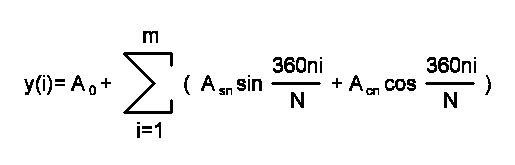
где Ao - постоянная составляющая исследуемой функции y(i), Asn и Acn соответственно синусные и косинусные составляющие гармонических составляющих спектра, а m - число гармоник спектра, которое, согласно теореме Котельникова, равно половине дискретных отсчётов, то есть m
Коэффициенты Asn и Acn можно рассчитать численным методом прямоугольников,
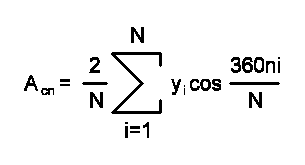
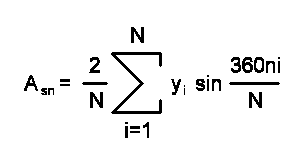
а An равно геометрической сумме Asn и Acn:
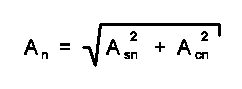
По вышеописанным формулам написана несложная программа для МК-161:
0 1 2 3 4 5 6 7 8 9 00 П7 П8 1 4 П8 П4 Сх В↑ ИП7 ИП0 10 - С/П КП4 FL0 06 ИП7 2 ÷ К[х] П9 20 1 /-/ Farccos 2 х ИП7 ÷ ПА ИП9 П1 30 ИП7 П0 ИП8 П4 Сх ПП 88 Fsin КИП4 х 40 + FL0 35 2 ИП7 ÷ х ПD ИП7 П0 50 ИП8 П4 Сх ПП 88 Fcos КИП4 х + FL0 60 53 2 ИП7 ÷ х ПЕ Fх2 ИПD Fх2 + 70 F√ ПС Сх В↑ ИП9 ИП1 - ИПС С/П FL1 80 30 Сх В↑ В↑ В↑ С/П БП 00 ИП9 ИП1 90 - ИП7 ИП0 - 1 + х ИПА х В/О
Перед запуском программы в регистр вводим количество дискретных отсчётов, N->РХ и запускаем программу, В/О, С/П. После запуска программы, в регистре РХ отображается номер дискретного отсчёта исследуемой функции, начиная с 0-го.
Вводим значение 0-го дискретного отсчёта и нажимаем клавишу С/П. После этого, в регистре РХ отображается номер следующего отсчёта, вводим его значение и нажимаем клавишу С/П. Таким образом вводим все дискретные отсчёты исследуемой функции и запускаем программу клавишей С/П.
После останова в регистре РY находится номер гармоники, а в регистре РХ амплитуда этой гармоники. В первую очередь выводится удвоенное значение постоянной составляющей исследуемой функции, как расчётное значение 0-й гармоники. Нажимаем клавишу С/П и получаем расчётное амплитудное значение 1-й гармоники спектра исследуемой функции, последующими нажатиями клавиши С/П будем получать амплитуды следующих гармоник спектра, вплоть до (N/2-1)-й. Расчёт окончен. Нажав клавишу С/П, снова переходим к вводу числа дискретных отсчётов. Можно исследовать спектр новой функции по её дискретным отсчётам.
Например, можно рассчитать гармонический спектр функции, заданной 24-мя дискретными отсчётами, указанных в таблице:

Расчётные значения амплитуд гармоник спектра помещены в таблице:

Примечания. Ао=0. Удвоенное значение постоянной составляющей функции равна нулю, то есть функция не имеет постоянной составляющей. Расчётные амплитуды чётных гармоник спектра получились меньше 10^-13, то есть значительно меньше амплитуд нечётных гармоник, по этому в таблице расчётные амплитуды чётных гармоник указаны равными нулю.
Дополнительно рассчитаем гармонический спектр ряда функций, заданных 24-мя дискретными отсчётами, указанными в таблицах.
1. Функция синусоидального сигнала, длительностью в один период:

Её расчётный спектр:
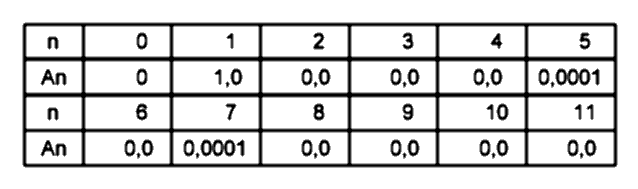
Видно, что спектр не имеет постоянной составляющей и состоит преимущественно 1-й гармоники с амплитудой А1=1,0. Значения амплитуд 5-й и 7-й гармоник, составляют около 0,01% от амплитуды 1-й гармоники. Это вызвано погрешностью введённых отсчётов.
2. Функция синусоидального сигнала, длительностью в половину периода:

Её расчётный спектр:
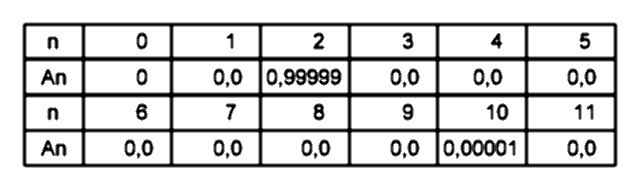
Спектр не имеет постоянной составляющей и состоит преимущественно 2-й гармоники с амплитудой А2=0,99999. Значение амплитуды 10-й гармоники, составляет около 0,001% от амплитуды 2-й гармоники.
3. Функция синусоидального сигнала, длительностью в треть периода:

Её расчётный спектр:
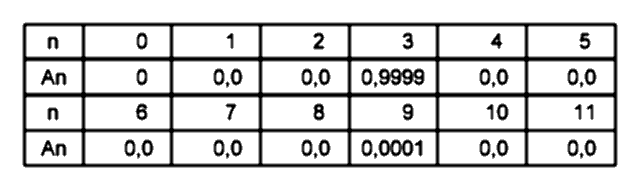
Спектр не имеет постоянной составляющей и состоит преимущественно 3-й гармоники с амплитудой А3=0,9999. Значение амплитуды 9-й гармоники, составляет около 0,01% от амплитуды 3-й гармоники.
4. Функция суммы синусоидальных сигналов, длительностями один период, в половину и треть периода:

Её расчётный спектр:
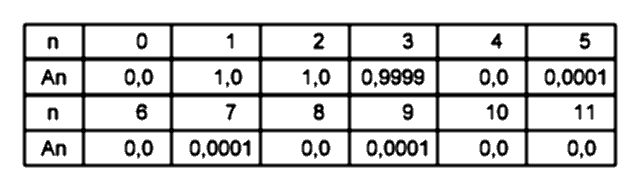
Спектр не имеет постоянной составляющей и состоит преимущественно 1-Й, 2-й, 3-й гармоник с амплитудами А1=1,0, А2=1,0, А3=0,9999. Значения амплитуд 5-й, 7-й и 9-й гармоник, составляет около 0,01% от амплитуд основных гармоник сигнала.
5. Функция сигнала однополупериодного выпрямителя:

Её расчётный спектр:

Спектр имеет удвоенную постоянную составляющую, равную 0,633, то есть действующее напряжение на выходе выпрямителя будет равным (0,633/0,707)/2=0,4476 от действующего напряжения на входе выпрямителя. Из-за однополупериодного выпрямления, в спектре есть 1-я гармоника, других нечётных гармоник в спектре выпрямленного напряжения нет.
6. Функция сигнала двухполупериодного выпрямителя:

Её расчётный спектр:

Спектр имеет удвоенную постоянную составляющую, равную 1,266, то есть действующее напряжение на выходе выпрямителя будет равным (1,266/0,707)/2=0,8952 от действующего напряжения на входе выпрямителя. Нечётных гармоник в спектре выпрямленного напряжения нет.
7. Функция сигнала с прямоугольной формой (симметричного меандра):

Её расчётный спектр:

Спектр не имеет постоянной составляющей и состоит только из нечётных гармоник.
Количество дискретных отсчётов хранится в регистре Р7, смещение косвенной адресации значений дискретных отсчётов в регистре Р8, количество гармонических составляющих спектра в регистре Р9, дискретность отсчётов в регистре РА, а значения дискретных отсчётов хранятся в регистрах, начиная с Р15 и до Р(14+N). Таким образом, количество дискретных отсчётов, по которым программа может рассчитать гармонический спектр исследуемой функции, достигает 984. Правда, увеличение числа дискретных отсчётов функции значительно увеличивает время расчёта, из-за того, что время расчёта гармонического спектра прямо пропорционально квадрату количества дискретных отсчётов.
Сайт работает на микрокомпьютере 


